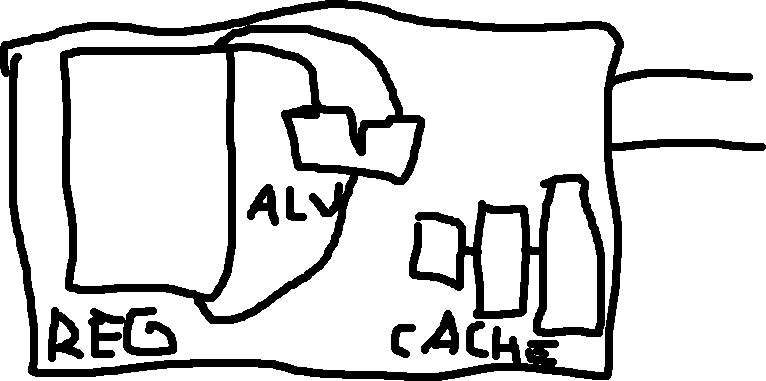
Constructing a CPU

Constructing a CPU:

1. Add Register Bank/File
2. Add ALU (Arithmetic Logic Unit)
   • It must be able to read input from reg.
   • It must be able to write to reg.
3. Add Cache
   • We can have multiple levels of cache.
   • Important for taking instructions from outside the CPU into the CPU across the data bus.

On I/O: There are only two ways for external devices to communitate with the CPU:

1. Interrupt: Stop what you’re doing and respond.
2. Reject means do nothing.
3. Accept means respond.
4. Delay means delay.
5. Polling: Periodically ask each device if they have input.

• Parallel Polling: “Does anybody have a question?”
  • In this case, you have to decide on priority of responding.

Interrupt v. Polling: If a device fails, interrupt won’t catch it.

Computer Architecture

Different Instruction Formats Require Different CPU Architectures

Suppose this operand format:

AC <- AC + 100

The realization of this may result in a huge delay if the same memory cell is required for the next instruction.

Thus, it’s better to use an intermediate register to save the possible required data.

Memory-Memory Architectures (Harvard)

Operation Operand1, Operand2, Operand3, Next Instruction

• In this architecture, the programmer manually sets the next address.

Operation Operand1, Operand2, Operand3

• The PC defines the next instruction.

Operation Operand1, Operand2

• Operand1 can be a source and a destination.

Register-Memory Architectures (Harvard)

Operation Operand

• Accumulator, the default operand, is source and destination.

Register-Memory Architectures (Von Neumann)

Operation Operand

• Uses MAR and MDR (memory address/data register) to work with one bus.

Simple Fetch Architecture

Fetch: During the fetch cycle, the CPU retrieves the instruction from memory.

• PC typically points to instruction, and increments after execution.

Instruction Fetch:

• An instruction pointed by the PC is loaded from main memory into the PC before getting incremented by 4, because the word size is 4 bytes.

Instruction Decode

1. Find out what is the instruction
2. Access register to read parameters.

How to Speed Up Computers

Superscaling

Until now, we’ve been using specialized modules for fetching, decoding, executing, and writeback.

Now, suppose we instead get 4 modules who can do all operations.

Limitation: Instruction dependency. You can’t write a program where all the instructions aren’t related.

External Cache

The main memory is very slow, one solution is to add an external cache.

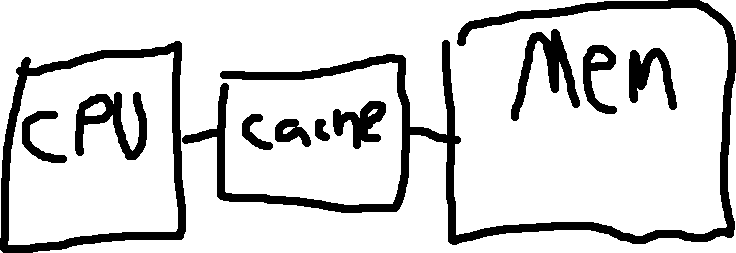
Suppose it takes:

• \tau_2 ns for data to travel from main memory to cache, and
• \tau_1 ns for data to travel from cache to CPU.
• h: Hit ratio: Fraction of memory accesses that are satisfied by the cache.
  • 1-h: When we want to find something, and it isn’t in the cache.

The average access time (AAT) would be

h\tau_1 + (1-h)t_2

• First term is when we find the data we want in the cache. Second term is when we have to look into main memory.
• Note: This formula is a lie.

For example, suppose h = 0.9, t_1 = 1, t_2 = 100

\text{AAT} = 0.9 \times 1 + 0.1 \times 100 = 10.9

Professor’s Personal Experience: In the real world, the hit ratio lies between 0.7 and 1.0

The lie: If we have to go to main memory, we’ll actually need to go in and pull the data out, which means we’ll be traveling across t_1 and t_2

\boxed{ \text{AAT: } h\tau_1 + (1-h)(t_1 + t_2) }

If we plug in h = 0.9, t_1 = 1, t_2 = 100, we’d get:

0.9 * 1 + (0.1)(101) = 11

Q: Why can’t we put the cache in the CPU?

A: Space.

CISC v. RISC:

• CISC: Complex Instruction Set Computers
• RISC: Reduced Instruction Set Computers

ADD AX,1 # ADD is a general instruction
INC AX   # INCREMENT is not a general instruction

• INC would be provided in CISC, but not in RISC.

RISC can increase space in the CPU.

• 80% of a program is typically with 20% of the instruction set.
  • And any missing functionality can be constructed if needed.
• This is why we are moving towards RISC in the real-world.

By switching to CISC, we can put cache in the CPU.

Not only that, but we can split up the cache into a smaller and bigger cache:

• The smaller cache is faster than the bigger cache.
• This split is good because, once again, a minority of instructions are used a lot, so they can be put into L1 cache.
• In short, having levels of cache beats having a single large cache.

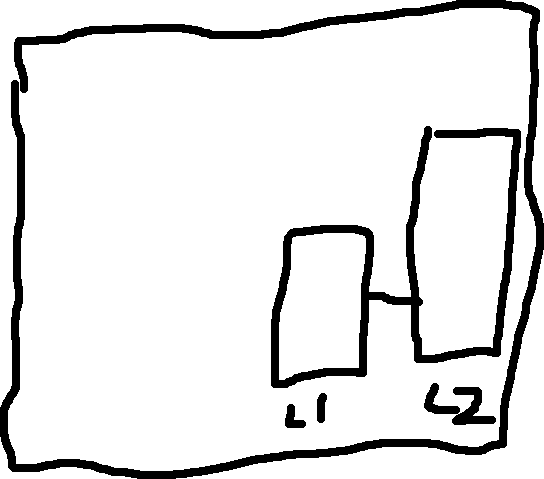
Accessing cache is random.

• Q: What is the difference between cache and a high speed main memory?
  • e.g., imagine they are the same speed; what would the difference be?
• A: Cache is CAM (Content Addressable Memory) and inside the CPU.

On CAM

• Suppose we have 8 memory cells.
  • With three bits, we can address every cell (0, 1, …, 7)

• All memories work like this, but CAM has the ability to search the memory for content and get the address.
• e.g., CAM(00001001) => 0x6. If the content can be found in multiple banks, the result will depend on the algorithm used.

The technology of the cache and the CPU must be the same. * e.g., if the CPU is 1nm, the cache must also be 1nm. * Technically, the CPU can be larger than the cache, but it’ll be a waste of money. + e.g., 1nm CPU and 0.5 nm cache is valid, but wasteful.